4. 에퀴티 (Equity)

머리말

이 글은 포커를 제대로 배우고자 하는 모든 이들에게,

용어도 모르는 입문자부터 익숙한 플레이어들까지 쉽게 이해하고 적용할 수 있게끔 작성된 글임을 밝힙니다.

 

여러분이 레귤러(regular: 안정적으로 수익을 내는 플레이어)의 위치에 서고,

추가로 자신만의 전략을 연구하고 엣지를 가지는 플레이어로 거듭날 수 있기를 바랍니다.

---

이번에는, 에퀴티(equity)에 대해서 알아보도록 하겠습니다.

우선 에퀴티라는 게 뭘까요?

이전 글에서 짧게 나왔었는데, 쉽게 말하면 '현재 이길 수 있는 확률' 이라고 말할 수 있겠습니다.

 

EQUITY

다르게도 말하면 '팟에 속해있는 지분' 이라고도 표현하는데요,

중요한 점은 포커를 수학적으로 설명하기 위해 계산된 확률이라는 것입니다.

 

에퀴티를 계산해보는 것은 흥미롭고 즐거운 일이라고 말할 수 있어요.

내가 상대의 핸드, 레인지에 대해 몇 %의 승률을 가지고 있는 지,

나의 베팅과 콜이 수익적인 지,

이러한 것들을 계산하기 위해서 필요한 수치이기도 합니다.

 

늘 그렇듯 간단한 예시를 통해서 최대한 이해하기 쉽게끔 풀어보도록 하겠습니다.

 

---

 

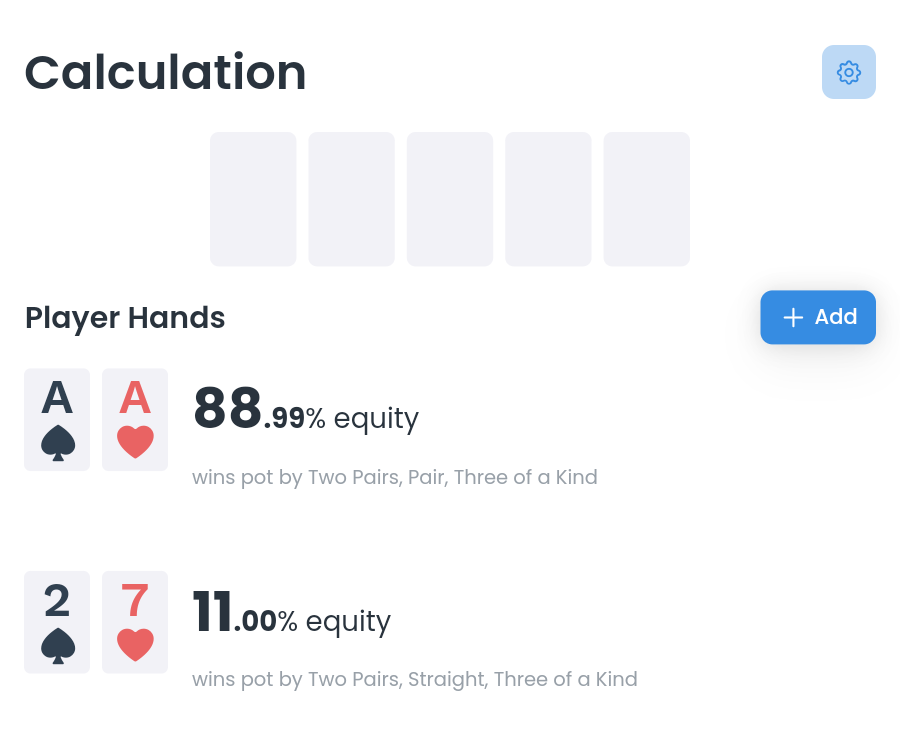
Preflop - AA vs 27o

예시를 가져왔습니다, 프리플랍 상황에서 에어라인과 27o의 승률을 비교해보면

AA는 약 89%의 에퀴티를 가지고, 27o은 약 11%의 에퀴티를 가집니다.

이러한 싸움을 10번 반복한다고 가정했을 때, 9:1 정도의 승률이 나온다는 소리겠죠?

 

Flop - AA vs 27o, Kd 7d 2h

이러한 에퀴티는 상황에 따라 변합니다.

플랍이 열리고 [ Kd 7d 2h ], 다음과 같은 카드가 보드가 떨어졌습니다.

 

AA는 A 원 페어, 27o은 7, 2 투 페어로 27o이 더 강한 족보를 만들게 된 상황을 볼 수 있습니다.

여기서 AA는 약 25%의 에퀴티를 가지고, 27o은 약 75%의 에퀴티를 가집니다.

이러한 싸움을 10번 반복한다고 가정했을 때는, 1:3 정도의 승률이 나오겠죠?

 

Turn - AA vs 27o, Kd 7d 2h Js

이후 턴에서는 J 스페이드(Js라고도 표현)가 보드에 떨어졌습니다, [ Kd 7d 2h Js ].

플랍에서와 상황은 동일합니다, A 원 페어와 7,2 투페어로 27o이 이기고 있는 상황입니다.

 

여기서 AA는 약 18%의 에퀴티를 가지고, 27o은 약 82%의 에퀴티를 가집니다.

이러한 싸움을 10번 반복한다고 가정했을 때는, 1:4 정도의 승률이 나오겠죠?

 

이제 남은 카드는 리버에서 떨어지는 1장의 카드밖에 없습니다.

리버에서 어떤 카드가 떨어져야 AA가 이길 수 있을까요?

이러한 질문에 답할 수 있는 카드를 아웃츠(outs: 승자로써의 가능성을 높여주는 카드)라고 합니다.

 

우리는 이러한 아웃츠를 바로 계산할 수 있겠죠, 하나씩 살펴보면:

 

• A가 떨어지는 경우, Three of a Kind - A Set
• K가 떨어지는 경우, Two Pair - A, K
• J가 떨어지는 경우, Two Pair - A, J

 

이렇게 3가지 경우가 존재합니다.

K나 J가 떨어지게 되면, 27o은 7, 2 투 페어가 아닌 K, 7 투 페어, J, 7 투 페어로 족보가 완성되기 때문에 A, K 투 페어, A, J 투 페어를 상대로 지게 되겠죠? (쓰리 페어는 없다는 사실을 기억하세요, 족보는 항상 5장으로 완성됩니다!)

 

그리고 각각의 카드는 콤보로 존재하게 되겠죠, 조합론을 기억하고 계시리라 믿습니다 :)

결국 아웃츠는 총 8장으로 다음과 같습니다:

 

• Ad, Ac, Ks, Kh, Kc, Jh, Jd, Jc

 

즉, 44장의 카드 중에서 8장의 카드가 나올 확률임을 알 수 있습니다, 8/44로 약 18.2%가 나오게 됩니다.

총 52장의 카드 중에서 커뮤니티 카드 4장, 서로의 핸드 2장씩이 빠지게 되어 44장의 카드가 형성된다는 사실,

확실한 정보만이 이러한 계산에 영향을 주게 됩니다.

만약 오픈된 카드 1장이 Ad임을 확인했다면, 43장의 카드 중에서 7장의 카드를 뽑을 확률로 변하게 되겠죠.

 

또한 불확실한 정보로 인해 계산이 틀릴 수도 있다는 사실을 알고 계셔아 합니다.

아웃츠로 본 카드가 아웃츠가 아닐 수도 있고, (내 족보를 발전시키지만 그와 동시에 상대의 족보도 발전시키는 경우)

아웃츠가 덱에 존재하지 않을 수도 있습니다. (다른 플레이어들이 가지고 있는 경우)

 

이는 실제 플레이를 하면서 항상 생각해야할 요소이며, 여기서는 고려하지 않아도 되는 요소겠죠.

중요한 내용이니 꼭 이해하고 넘어가도록 합시다.

 

River - AA vs 27o, Kd 7d 2h Js Ac

리버 온 더 에이스! 역시 홀덤 아니랄까봐 에이스가 떡하니 등장해버렸습니다, [ Kd 7d 2h Js Ac ].

이제는 상황이 달라졌습니다, AA는 A 셋(set: 파켓을 들고 트리플 족보를 만든 경우 셋이라고 지칭)을 만들었습니다.

27o은 7, 2 투 페어로 이대로 쇼다운한다면 AA가 승리하겠죠.

 

여기서 AA는 100%의 에퀴티를 가집니다, 더 뽑을 카드가 없기 때문입니다.

결국 리버까지 간다면 최종적으로 가지는 에퀴티는 3가지 경우밖에 없습니다:

 

• 이기거나 (Win)
• 지거나 (Lose)
• 비기거나 (Tie)

 

이제는 에퀴티가 어떻게 계산되는 지 알 수 있겠죠? 좋아요.

 

이처럼 실질적으로 리버에서는 정해진 에퀴티를 가지게 되지만, 중요한 사실이 존재합니다.

내가 확실히 이기고 있는 지, 지고 있는지는 상대의 핸드를 보는 것이 아닌 이상 알 수 없겠죠? (넛 제외)

그렇기 때문에 우리는 상대의 레인지에 대해서 몇 %의 승률을 가지는 지와 같은 형태로 접근할 수 있습니다.

 

위의 예제에서 우리가 AA일 때, 상대가 레인지의 8%로 Q10과 같은 콤보를 가지고 있다고 해볼까요?

제외한 나머지를 이긴다고 가정해본다면, 상대의 레인지에 대해 92%의 에퀴티를 가지고 있다고도 말할 수 있는거죠.

(물론 실제 에퀴티는 비기는 경우를 제하고 100%거나 0%지만, 레인지에 대한 에퀴티임을 이해하셔야 합니다!)

 

또한 이러한 아웃츠를 계산하기 위해서 만들어진 간단한 공식이 있습니다.

플랍에서 리버까지는 아웃츠 * 4 - 1

Flop to River: outs*4-1 = equity%

 

턴에서 리버까지는 아웃츠 * 2

Turn to River: outs*2 = equity%

 

어디까지나 오차는 존재하지만 빠르게 대략적인 에퀴티를 계산할 수 있기에 사용되는 공식입니다.

 

예를 들어서 플랍에서의 아웃츠를 8장으로 본다면, 리버까지의 에퀴티는 8*4-1 = 35%

이렇게 구해볼 수 있습니다.

 

+

 

이러한 공식으로 하여금 우리는 플랍에서 리버까지 핸드가 메이드될 확률을 계산할 수 있겠죠?

FD*의 경우, 하나의 문양에 대해 9장의 아웃츠를 가지기 때문에 약 35%의 확률로 메이드 됩니다.

OESD*의 경우, 8장의 아웃츠를 가지기 때문에 약 31%의 확률로 메이드 됩니다.

GSSD*의 경우, 4장의 아웃츠를 가지기 때문에 약 15%의 확률로 메이드 됩니다.

1V*의 경우, 3장의 아웃츠를 가지기 때문에 약 11%의 확률로 메이드 됩니다.

2V*의 경우, 6장의 아웃츠를 가지기 때문에 약 23%의 확률로 메이드 됩니다.

 

당연하게도, 이러한 특성은 중첩될 수 있습니다.

FD+2V의 경우, 13장의 아웃츠를 가지기 때문에 약 51%의 확률로 메이드 됩니다.

(15장의 아웃츠가 아닌 이유는, FD와 2V가 동시에 공유하는 아웃츠가 있기 때문입니다!)

GSSD+1V의 경우, 7장의 아웃츠를 가지기 때문에 약 27%의 확률로 메이드 됩니다.

FD+OESD의 경우, 15장의 아웃츠를 가지기 때문에 약 59%의 확률로 메이드 됩니다.

 

해당 확률은 위의 공식을 사용해서 나온 대략적인 수치임을 기억하세요! 어느정도의 오차가 존재합니다.

 

별개로 턴과 리버에 필요한 카드가 모두 떨어져야 메이드되는 경우가 있겠죠?

이런 경우를 백도어(backdoor), 혹은 러너러너(runner-runner)라고 부릅니다.

 

예를 들어서 다음과 같은 보드가 있습니다 [ As Jc 6d ].

우리가 Kc5c를 가지고 있다면 BDFD(backdoor flush draw), BDSD(backdoor straight draw)를 가지게 되는 거죠.

확률 또한 계산해 볼 수 있겠죠, BDFD부터 보면 10/47*9/46로 약 4%의 확률을 가지게 되고,

BDSD를 보면 8/47*4/46로 약 1.5%의 확률을 가진다고 볼 수 있습니다.

BDSD가 OESD의 형태로 메이드 되는 경우에는 8/47*8/46의 확률이겠죠.

 

*FD (flush draw: 플러시 메이드까지 한 장 남은 경우)

*OESD (open-ended straight draw: 위 아래로 스트레이트 메이드 카드를 가지는 경우)

*GSSD (gutshot straight draw: 중간으로 한장의 스트레이트 메이드 카드를 가지는 경우)

*1V (one overcard: 보드의 가장 높은 카드보다 높은 카드를 핸드에 한 종류 가지고 있는 경우)

*2V (two overcard: 보드의 가장 높은 카드보다 높은 카드를 핸드에 두 종류 가지고 있는 경우)

 

---

 

추가로 자주 쓰이는 용어 중 폴드 에퀴티(fold equity)라는 용어가 있습니다.

폴드 에퀴티를 이해하는 것 또한 정말 중요합니다! 한 번 알아보자고요.

 

정의부터 알아보면, 폴드 에퀴티는 플레이어가 베팅이나 레이즈에 폴드할 확률을 말합니다.

만약 여러분이 베팅이나 레이즈에 대해서 상대방이 폴드할 것인지 생각해본 적이 있다면, 이미 이러한 개념을 적용해본 것입니다.

 

question de bluff

결국 이 개념은 많은 경우에 블러프(bluff: 패를 속이는 행위)를 결정함에 있어서 적용됩니다.

우리는 당연하게도 EV를 가지는 블러프를 해야하기 때문에, 이러한 개념이 존재하는 것이죠.

 

만약 우리의 에퀴티가 0%라고 가정해보면, 팟을 가져오기 위해선 상대를 폴드시키는 것이 유일한 방법이 되겠죠?

그렇기 때문에 베팅 혹은 레이즈를 위험, 팟을 보상이라고 보면, 보상에 대한 위험률이 존재합니다.

폴드 에퀴티가 보상에 대한 위험률보다 높다면, EV를 가지는 블러프라고 볼 수 있게 되는 것입니다.

 

위험 대비 보상 비율을 구하기 위한 공식을 계산해볼 수 있겠죠.

보상에 대한 위험률 = [벳/(벳+벳 이전의 팟)]x100

 

예시를 위해 10,000의 팟에 2,500을 베팅했다고 가정해보면 다음과 같겠죠.

보상에 대한 위험률 = [2,500/(2,500+10,000)]x100
보상에 대한 위험률 = 2,500/10,000x100
보상에 대한 위험률 = 0.2x100
보상에 대한 위험률 = 20%

 

즉, 이러한 상황은 이렇게 해석할 수 있게 되는거죠,

상대가 콜 했을때의 에퀴티가 0%일 때, 10,000의 팟에 2,500을 베팅하는 것이 수익적인 블러프가 되려면 20%보다 높은 폴드 에퀴티가 필요로 하는구나.

 

하지만 내 에퀴티가 0%가 아니라 더 높을 경우, EV를 가지는 베팅을 위한 폴드 에퀴티는 줄어들게 됩니다.

간단한 이유죠! 상대가 콜 했다고 해도 내가 이길 확률이 존재하기 때문입니다.

다시 한 번 요약하면, 에퀴티가 높을수록 필요한 폴드 에퀴티는 줄어들게 됩니다.

 

FD, OESD와 같은 드로우 핸드들로 블러프하는 것을 세미 블러프(semi-bluff)라고 합니다.

이러한 핸드들이 에퀴티를 가지면서도 폴드 에퀴티를 가지고 플레이하는 대표적인 핸드라고 볼 수 있겠습니다.

 

폴드하면 팟을 싸우지 않고 가져올 수 있으니 좋고,

콜해도 임플라이드 오즈와 함께 이길 수 있는 확률이 있으니 좋은 거죠.

 

임플라이드 오즈(implied odds)는 쉽게 말해 잠재적인 배당을 뜻하는 데요,

이는 이후에 팟 오즈(pot odds)와 함께 배워보도록 하겠습니다.

 

---

 

이번 글에서는 에퀴티와 아웃츠, 폴드 에퀴티에 대해서 알아보았습니다.

에퀴티를 가진다는 것이 어떤 의미인지, 폴드 에퀴티를 가진다는 것이 어떤 의미인지 이해하셨으면 좋겠습니다.

 

'내 핸드는 지금 상대 레인지에 대해 80%의 에퀴티를 가지고 있어.'

'내 아웃츠는 6장이고, 리버까지 약 23%의 에퀴티를 가지고 있어.'

 

또한 이후에 베팅에서도 다뤄질 내용이지만,

폴드 에퀴티에 대해서도 꼭 고민해보시길 바랍니다.

 

'더 크게 베팅하는 것이 더 많은 폴드 에퀴티를 만들까?'

'작게 베팅해도 충분한 폴드 에퀴티가 존재할까?'

'상대에게 폴드 에퀴티가 존재할까?'

 

항상 끊임없이 생각하고 질문해야 한다는 사실을 상기시켜 드리면서 글을 마치겠습니다.

 

나는 생각한다, 고로 존재한다.
- Rene Descartes